Назад | Оглавление | Домой | Далее
При реализации всех обсуждавшихся алгоритмов удаления невидимых линий и поверхностей устанавливались приоритеты, т. е. глубины объектов сцены или их расстояния от точки наблюдения. Алгоритмы, использующие список приоритетов, пытаются получить преимущество посредством предварительной сортировки по глубине или приоритету. Цель такой сортировки состоит в том, чтобы получить окончательный список элементов сцены, упорядоченных по приоритету глубины, основанному на расстоянии от точки наблюдения. Если такой список окончателен, то никакие два элемента не будут взаимно перекрывать друг друга. Тогда можно записать все элементы в буфер кадра поочередно, начиная с элемента, наиболее удаленного от точки наблюдения. Более близкие к наблюдателю элементы будут затирать информацию о более далеких элементах в буфере кадра. Поэтому задача об удалении невидимых поверхностей решается тривиально. Эффекты прозрачности можно включить в состав алгоритма путем не полной, а частичной корректировки содержимого буфера кадра с учетом атрибутов прозрачных элементов.
Для простых элементов сцены, например для многоугольников, этот метод иногда называют алгоритмом художника, поскольку он аналогичен тому способу, которым художник создает картину. Сначала художник рисует фон, затем предметы, лежащие на среднем расстоянии, и, наконец, передний план. Тем самым художник решает задачу об удалении невидимых поверхностей, или задачу видимости, путем построения картины в порядке обратного приоритета.
Для простой сцены, вроде той, что показана на рис. 5.13, а, окончательный список приоритетов можно получить непосредственно. Например, эти многоугольники можно упорядочить по их максимальному или минимальному значению координаты z. Однако уже для сцены, показанной на рис. 6.13 b, окончательный список приоритетов по глубине невозможно получить простой сортировкой по z. Если P и Q с рис. 5.13, b упорядочены по минимальному значению координаты z (zmin), окажется, что Р в списке приоритетов по глубине будет стоять перед Q. Если их записать в буфер кадра в таком порядке, то получится, что Q частично экранирует P. Однако фактически P частично экранирует Q. Правильный порядок в списке приоритетов будет тогда, когда P и Q поменяются местами.
Рис. 5.13. Установление приоритетов для многоугольников
Другие трудности показаны на рис. 5.14. Здесь многоугольники циклически перекрывают друг друга. На рис. 5.14, а P находится впереди Q, который лежит впереди R, который, в свою очередь, находится впереди P. На рис. 5.14, b P экранирует Q, a Q экранирует P. Аналогичное циклическое экранирование возникает при протыкании многоугольников; например, на рис. 5.12 показано, как треугольник протыкает прямоугольник. Там прямоугольник экранируется треугольником, и наоборот. В обоих примерах окончательный список приоритетов невозможно установить сразу. Выход из положения заключается в циклическом разрезании многоугольников по линиям, образованным пересечениями их плоскостей, до тех пор, пока не будет получен окончательный список приоритетов. Такие линии показаны пунктиром на рис. 5.14.
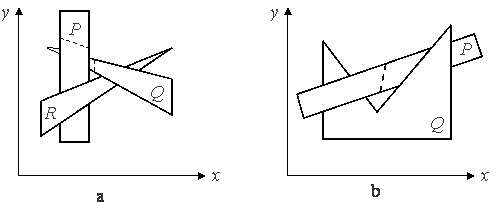
Рис. 5.14. Циклически перекрывающие многоугольники
Ньюэл М., Ньюэл Р. и Санча предложили специальный метод сортировки для разрешения конфликтов, возникающих при создании списка приоритетов по глубине. Этот метод включен в состав алгоритма Ньюэла - Ньюэла - Санча, который излагается ниже. В алгоритме динамически вычисляется новый список приоритетов перед обработкой каждого кадра сцены. Не накладывается никаких ограничений на сложность сцены и на тип многоугольников, используемых для описания элементов сцены. Первоначальный алгоритм Ньюэла - Ньюэла - Санча был предназначен для обработки трехмерных тел. Это расширение не ограничено рамками многогранников. Оно может, кроме того, обрабатывать тела смешанных типов в рамках одной сцены.
Сформировать предварительный список приоритетов по глубине, используя в качестве ключа сортировки значение zmin для каждого многоугольника. Первым в списке будет многоугольник с минимальным значением zmin. Этот многоугольник лежит дальше всех от точки наблюдения, расположенной в бесконечности на положительной полуоси z. Обозначим его через P, а следующий в списке многоугольник - через Q. Для каждого многоугольника P из списка надо проверить его отношение с Q.
Если ближайшая вершина Р (
)
будет дальше от точки наблюдения, чем самая удаленная вершина Q (
),
т. е. 
≥
никакая
часть P не может экранировать Q. Занести Р в буфер кадра
(см. рис. 5.13, а).
Если <
,
то Р потенциальное экранирует не только Q, но также и любой другой
многоугольник типа Q из списка, для которого
<.
Тем самым образуется множество {Q}. Однако Р может фактически и не
экранировать ни один из этих многоугольников. Если последнее верно, то Р
можно заносить в буфер кадра. Для ответа на этот вопрос используется серия
тестов, следующих по возрастанию их вычислительной сложности. Эти тесты ниже
формулируются в виде вопросов. Если ответ на любой вопрос будет положительным,
то Р не может экранировать {Q}. Поэтому Р сразу же
заносится в буфер кадра. Вот эти тесты:
¨ Верно ли, что прямоугольные объемлющие оболочки Р и Q не перекрываются по х?
¨ Верно ли, что прямоугольные оболочки Р и Q не перекрываются по у?
¨ Верно ли, что Р целиком лежит по ту сторону плоскости, несущей Q, которая расположена дальше от точки наблюдения (рис. 5.15, а)?
¨ Верно ли, что Q целиком лежит по ту сторону плоскости, несущей P, которая ближе к точке наблюдения (рис. 5.15, b)?
¨ Верно ли, что проекции Р и Q не перекрываются?
Рис. 5.15. Тесты для перекрывающихся многоугольников
Каждый из этих тестов применяется к каждому элементу {Q}. Если ни один из них не дает положительного ответа и не заносит Р в буфер кадра, то Р может закрывать Q.
Поменять Р и Q местами, пометив позицию Q в списке. Повторить тесты с новым списком. Это дает положительный результат для сцены с рис. 5.13, b.
Если сделана попытка вновь переставить Q, значит, обнаружена ситуация циклического экранирования (см. рис. 5.14.). В этом случае Р разрезается плоскостью, несущей Q, исходный многоугольник Р удаляется из списка, а его части заносятся в список. Затем тесты повторяются для нового списка. Этот шаг предотвращает зацикливание алгоритма.
Назад | Оглавление | Домой | Далее