Заполнение многоугольников
Рассмотрим, каким образом можно заполнить многоугольник, задаваемый замкнутой ломаной линией без самопересечений.
Простейший способ закраски многоугольника состоит в проверке принадлежности каждой точки этому многоугольнику. Более эффективные алгоритмы используют тот факт, что соседние пикселы, вероятно, имеют одинаковые характеристики (кроме пикселов граничных ребер). Это свойство называется пространственной когерентностью.

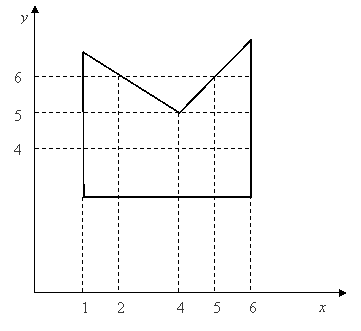
Рис. 2.9. Прохождение сканирующих строк по многоугольнику
В случае с многоугольником когерентность пикселей определяется вдоль сканирующей строки. Сканирующие строки обычно изменяются от «верха» многоугольника до его «низа». Характеристики пикселов изменяются только там, где ребро многоугольника пересекает строку. Эти пересечения делят сканирующую строку на области закрашенных и не закрашенных пикселов.
Рассмотрим, какие случаи могут возникнуть при делении многоугольника на области сканирующей строкой.
1.Простой случай. Например, на рис. 2.9 сканирующая строка y = 4 пересекает многоугольник при x = 1 и x = 6. Получается три области: x < 1; 1 ≤ x ≤ 6; x > 8. Сканирующая строка y = 6 пересекает многоугольник при x = 1; x = 2; x = 5; x = 6. Получается пять областей: x < 1; 1 ≤ x ≤ 2; 2 < x < 5; 5 ≤ x ≤ 6; x > 6. В этом случае x сортируется в порядке возрастания. Далее список иксов рассматривается попарно. Между парами точек пересечения закрашиваются все пикселы. Для y = 4 закрашиваются пикселы в интервале (1, 6), для y = 6 закрашиваются пикселы в интервалах (1, 2) и (5, 6).
2.Сканирующая строка проходит через вершину (рис. 2.10).

Рис. 2.10. Прохождение сканирующий строки через вершину
Например, по сканирующей строке y = 3 упорядоченный список x получится как (2, 2, 4). Вершина многоугольника была учтена дважды, и поэтому закрашиваемый интервал получается неверным: (2, 2). Следовательно, при пересечении вершины сканирующей строкой она должна учитываться единожды. И список по х в приведенном примере будет (2, 4).
3.Сканирующая строка проходит через локальный минимум или максимум (см. рис. 2.9 при y = 5). В этом случае учитываются все пересечения вершин сканирующей строкой. На рис. 2.9 при y = 5 формируется список x (1, 4, 4, 6). Закрашиваемые интервалы (1, 4) и (4, 6). Условие нахождения локального минимума или максимума определяется при рассмотрении концевых вершин для ребер, соединенных в вершине. Если у обоих концов координаты y больше, чем y вершины пересечения, то вершина – локальный минимум. Если меньше, то вершина пересечения – локальный максимум.
Для ускорения работы алгоритма используется список активных ребер (САР). Этот список содержит те ребра многоугольника, которые пересекают сканирующую строку. При пересечении очередной сканирующей строки вершины многоугольника, из САР удаляются ребра, которые находятся выше, и добавляются концы, которые пересекает сканирующая строка. При работе алгоритма находятся пересечения сканирующей строки только с ребрами из САР.