Часто возникает задача заполнения многоугольников, заданных набором вершин.
Задача заполнения многоугольников решается в два этапа:
1) сначала проводится операция отсечения многоугольника;
2) затем производится заполнение полученных многоугольников.
Этап отсечения необходим для определения реальных областей многоугольника, которые будут выведены на экран. Это необходимо, если многоугольник больше или выходит за пределы экрана или окна вывода.
Отсечение многоугольников
Отсечение многоугольников чаше всего проводится для отбрасывания частей многоугольника, выходящих за границу прямоугольной области, которая определяет экран или область окна. Однако отсечение может проводиться относительно и другого многоугольника. При этом порождается новый многоугольник или несколько новых многоугольников.
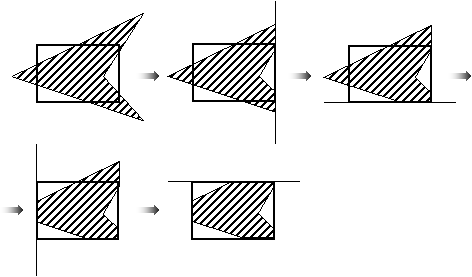
Рассмотрим алгоритм Сазерленда-Ходгмана (Sutherland-Hodgman). В алгоритме используется стратегия «разделяй и властвуй», которая позволяет решение общей задачи свести к решению ряда простых и похожих подзадач. Примером такой подзадачи является отсечение многоугольника относительно одной отсекающей границы. Последовательное решение четырех таких задач позволяет провести отсечение относительно прямоугольной области (рис. 2.7).

Рис. 2.7. Последовательное отсечение многоугольника
На вход алгоритма поступает последовательность вершин многоугольника V1, V2, …, Vn. Ребра многоугольника проходят от Vi к Vi+1 от Vn к V1. С помощью алгоритма производится отсечение относительно ребра и выводится другая последовательность вершин, описывающая усеченный многоугольник.
Алгоритм «обходит» вокруг многоугольника от Vn к V1 и обратно к Vn, проверяя на каждом шаге соотношение между последовательными вершинами и отсекающей границей. Необходимо проанализировать четыре случая:
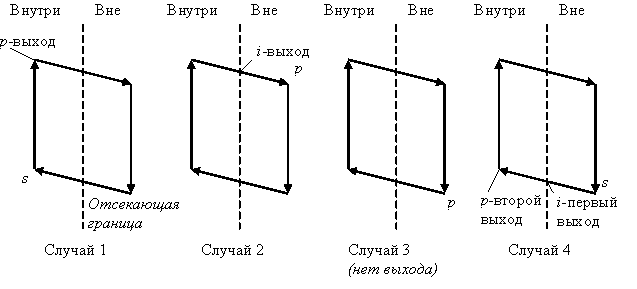
Рис. 2.8. Случаи, возникающие при отсечении многоугольников
Рассмотрим изображенное на рис. 2.8 ребро многоугольника, соединяющее вершину s с вершиной p. В первом случае ребро полностью лежит внутри отсекающей границы, к выходному списку добавляется вершина p. Во втором случае в качестве вершин выводится точка пересечения i, поскольку ребро пересекает границу, а начальная точка была выведена при анализе первого случая. В третьем случае обе вершины находятся за пределами границы и ни одна из них не выводится. В четвертом случае к выходному списку добавляется и точка пересечения i, и вершина p.
При отсечении многоугольника описанным алгоритмом возникает проблема, связанная с тем, что появляются ребра, частично совпадающие с границей окон. Лишние ребра можно устранить, введя дополнительную обработку или воспользовавшись более общим и более сложным алгоритмом Вейлера – Азертона.