Назад | Оглавление | Домой | Далее
Прежде чем перейдем к непосредственному рассмотрению возможности перевода математического описания объекта (линии и пр.) в растровую форму, рассмотрим понятие связности. Связность – возможность соединения двух пикселей растровой линией, т. е. последовательным набором пикселей. Возникает вопрос, когда пиксели (x1, y1) и (x2, y2) можно считать соседними. Для этого вводятся два понятия связности:
1. Четырехсвязность: пиксели считаются соседними, если либо их x-координаты, либо их y – координаты отличаются на единицу:
|x1 – x2| + |y1 – y2| ≤ 1;
2. Восьмисвязность: пиксели считаются соседними, если их x-координаты и y-координаты отличаются не более чем на единицу:
|x1 – x2| ≤ 1, |y1 – y2| ≤ 1.
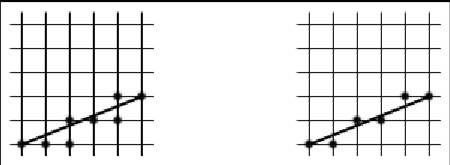
На рис. 2.2 изображены четырехсвязная и восьмисвязная линии.

Рис. 2.2. Четырехсвязная и восьмисвязная линии
При переводе объектов в растровое представление существуют, алгоритмы, как использующие четырехсвязность, так использующие восьмисвязность.
Назад | Оглавление | Домой | Далее