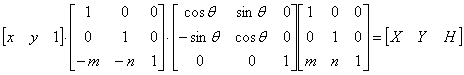 .
.
Назад | Оглавление | Домой | Далее
Выше было рассмотрено вращение изображения около начала координат. Однородные координаты обеспечивают поворот изображения вокруг точек, отличных от начала координат. В общем случае вращение около произвольной точки может быть выполнено путем переноса центра вращения в начало координат, поворотом относительно начала координат, а затем переносом точки вращения в исходное положение. Таким образом, поворот вектора положения [х у 1 ] около точки (т, п) на произвольный угол может быть выполнен с помощью преобразования
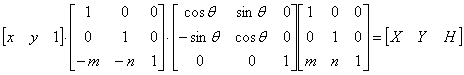 .
.
Выполнив две операции умножения матриц, можно записать
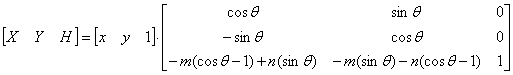
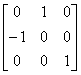
Предположим, что центр изображения имеет координаты (4, 3) и желательно повернуть изображение на 90° против часовой стрелки вокруг центральной его оси. Действие, выполненное с помощью матрицы
 ,
,
вызывает вращение вокруг начала координат, а не вокруг оси. Как сказано выше, необходимо вначале осуществить перенос изображения таким образом, чтобы желаемый центр вращения находился в начале координат. Это осуществляется с помощью матрицы переноса
 .
.
Затем следует применить матрицу вращения и, наконец, привести результаты к началу координат посредством обратной матрицы. Вся операция

может быть объединена в одну матричную операцию путем выполнения матричных преобразований вида
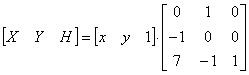 .
.
В результате будет получено х* =Х/Н и у* = Y/H. Двумерные вращения около каждой оси ортогональной системы представлены на рис. 3.5.
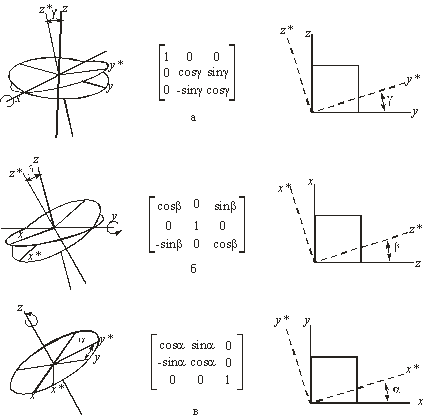
Рис. 3.5. Вращение: a — вокруг оси х; б — вокруг оси y; в — вокруг оси z
Назад | Оглавление | Домой | Далее