Назад |
Оглавление | Домой |
Далее
Существует три основных способа закраски объектов,
заданных полигональными сетками. В порядке возрастания сложности ими являются:
1)
однотонная закраска;
2)
метод Гуро (основан на интерполяции значений интенсивности);
3)
метод Фонга (основан на интерполяции векторов нормали).
В каждом из этих случаев может быть использована любая из
моделей закраски, описанная выше.
При однотонной закраске вычисляют один уровень
интенсивности, который используется для закраски всего многоугольника. При этом
предполагается, что:
-
Источник света расположен в
бесконечности, поэтому произведение (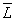
×
)
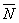постоянно на всей полигональной грани.
-
Наблюдатель находится в
бесконечности, поэтому произведение (×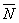
)
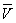постоянно на всей полигональной грани.
-
Многоугольник представляет
реальную моделируемую поверхность, а не является аппроксимацией
криволинейной поверхности. Если какое-либо из первых двух предположений
оказывается неприемлемым, можно воспользоваться усредненными значениями
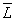и
,
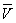вычисленными, например, в центре многоугольника.
Последнее предположение в большинстве случаев не
выполняется, но оказывает существенно большее влияние на получаемое изображение,
чем два других. Влияние состоит в том, что каждая из видимых полигональных
граней аппроксимированной поверхности хорошо отличима от других, поскольку
интенсивность каждой из этих граней отличается от интенсивности соседних граней.
Различие в окраске соседних граней хорошо заметно вследствие эффекта полос Маха.
Назад |
Оглавление | Домой |
Далее