Назад | Оглавление | Домой | Далее
Компьютерная геометрия есть математический аппарат, положенный в основу компьютерной графики. В свою очередь, основу компьютерной геометрии составляют различные преобразования точек и линий. При использовании машинной графики можно по желанию изменять масштаб изображения, вращать его, смещать и трансформировать для улучшения наглядности перспективного изображения. Все эти преобразования можно выполнить на основе математических методов, которые мы будем рассматривать далее.
Преобразования, как и компьютерную геометрию, разделяют на двумерные (или преобразования на плоскости) и трехмерные (или пространственные). Вначале рассмотрим преобразования на плоскости.
Для начала заметим, что точки на плоскости задаются с помощью двух ее координат. Таким образом, геометрически каждая точка задается значениями координат вектора относительно выбранной системы координат. Координаты точек можно рассматривать как элементы матрицы [x,y], т. е. в виде вектор-строки или вектор-столбца. Положением этих точек управляют путем преобразования матрицы.
Точки на плоскости xy можно перенести в новые позиции путем добавления к координатам этих точек констант переноса:
![]() .
.
Таким образом, для перемещения точки на плоскости надо к матрице ее координат прибавить матрицу коэффициентов преобразования.
Рассмотрим результаты матричного умножения матрицы [x,y], определяющей точку Р, и матрицы преобразований 2´2 общего вида:
![]() .
.
Проведем анализ полученных результатов, рассматривая x* и y* как преобразованные координаты. Для этого исследуем несколько частных случаев.
Рассмотрим случай, когда a = d = 1 и c = b = 0. Матрица преобразований приводит к матрице, идентичной исходной:
![]() .
.
При этом изменений координат точки Р не происходит.
Если теперь d = 1, b = c = 0, a = const, то:
![]() .
.
Как видно, это приводит к изменению масштаба в направлении х, так как х*=ах. Следовательно, данное матричное преобразование эквивалентно перемещению исходной точки в направлении х.
Теперь положим b = c = 0, т. е.
![]() .
.
В результате получаем изменение масштабов в направлениях x и y. Если a ≠ d, то перемещения вдоль осей неодинаковы. Если a = d >1, то имеет место увеличение масштаба координат точки Р. Если 0 < a=d <1, то будет иметь место уменьшение масштаба координат точки Р.
Если a или (и) d отрицательны, то происходит отображение координат точек. Рассмотрим это, положив b = c = 0; d = 1 и а = -1, тогда
![]() .
.
Произошло отображение точки относительно оси у. В случае b = c = 0, a = 1, d = -1, отображение происходит относительно оси х. Если b = c = 0, a = d < 0, то отображение будет происходить относительно начала координат.
Заметим, что отображение и изменение масштаба вызывают только диагональные элементы матрицы преобразования.
Теперь рассмотрим случай, когда a = d = 1, а с = 0, т. е.
![]() .
.
Координата х точки Р не изменяется, в то время как у* линейно зависит от начальных координат. Этот эффект называется сдвигом. Аналогично, когда a = d = 1, b = 0, преобразование осуществляет сдвиг пропорционально координате у.
Заметим, что преобразование общего вида, примененное к началу координат, не приведет к изменению координат точки (0,0). Следовательно, начало координат инвариантно при общем преобразовании. Это ограничение преодолевается за счет использования однородных координат.
Если подвергнуть общему преобразованию различные геометрические фигуры, то можно установить, что параллельные прямые преобразуются в параллельные прямые, середина отрезка – в середину отрезка, параллелограмм – в параллелограмм, точка пересечения двух линий – в точку пересечения преобразованной пары линий.
Преобразование единичного квадрата
Четыре вектора положения точек единичного квадрата с одним углом в начале координат записываются в виде
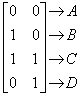
Применение общего матричного преобразования
![]()
к единичному квадрату приводит к следующему:
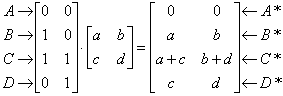 .
.
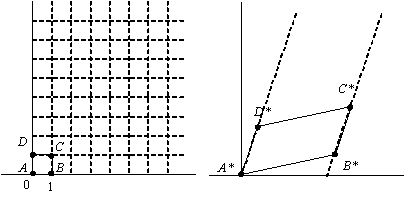
Рис. 3.1. Преобразования единичного квадрата
Из полученного соотношения можно сделать вывод, что координаты В* определяются первой строкой матрицы преобразования, а координаты D* второй строкой этой матрицы. Таким образом, если координаты точек В* и D* известны, то общая матрица преобразования определена. Воспользуемся этим свойством для нахождения матрицы преобразования для вращения на произвольный угол.
Общую матрицу 2´2, которая осуществляет вращение фигуры относительно начала координат, можно получить из рассмотрения вращения единичного квадрата вокруг начала координат.

Рис. 3.2. Вращение единичного квадрата
Как следует из рис. 3.2, точка В с координатами (1,0) преобразуется в точку В*, для которой х*=(1)cos q и y=(1)sin q, а точка D, имеющая координаты (0,1) переходит в точку D* с координатами x*=(-1)sin q и y*=(1)cos q.
Матрица преобразования общего вида записывается так:
![]() .
.
Для частных случаев. Поворот на 90° можно осуществить с помощью матрицы преобразования
![]() .
.
Если использовать матрицу координат вершин, то получим, например:
 .
.
Поворот на 180° получается с помощью матрицы
![]() .
.
Отображение
В то время как чистое двумерное вращение в плоскости xy осуществляется вокруг оси, перпендикулярной к этой плоскости, отображение определяется поворотом на 180° вокруг оси, лежащей в плоскости ху.
Такое вращение вокруг линии у = х происходит при использовании матрицы
![]() .
.
Преобразованные новые выражения определяются соотношением
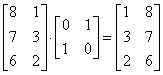 .
.
Вращение вокруг у = 0 получается при использовании матрицы
![]() .
.
Назад | Оглавление | Домой | Далее